Using cross multiplication method, solve 3 x 5 y = 2 5 7 x 6 y = 3 0 MEDIUM(Any two of 3 equations can be chosen for elimination of one of the variables) (b) Method of cross multiplication We write the equations as follows 2 x – y (z – 3) = 0 x 3y (–2z –11) = 0 By cross multiplication y 1 –1(–2z – 11) –3(z – 3) (z – 3)–2(–2z – 11) 2 3 –1(–1) x = = ´ y 1 = = z 5z19 7 x x = 7 z 1 Which of the following pairs of linear equations has unique solution, no solution, or infinitely many solutions In case there is a unique solution, find it by using cross multiplication method

7lsnwr9avofjvm
X y/2=4 x/3 2y=5 by cross multiplication method
X y/2=4 x/3 2y=5 by cross multiplication method- Solve(cross multiplication method) 2/x3/y=2 1/x1/2y=1/3 Maths Linear Equations in Two VariablesTo ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW 2x 3 y 3z =5 , x 2y z=4 , 3x y2z = 3




無料ダウンロード 3x 2y5 X5 Y
Solve each of the following systems of equations by using the method of cross multiplication 2 a x 3 b y = (a 2 b) 3 a x 2 b y = (2 a b) Medium View solution The area of a rectangle gets reduced by 9 square units if its length is reduced by 5 units and the breadth is increased by 3 units The Questions and Answers of 04x 03y=17 07x02y=08 7(y 3)2(X 2)=14 4(y2) 3(x3)=2 X y/2=4 X/3 2y=5 solve this in two min From substitution, elimination,and cross multiplication method? Using matrix method, solve the system of equations 3x 2y 2z = 3, x 2y 3z = 6, 2xy z = 2 asked in Class XII Maths by rahul152 ( 2,8 points) determinants
Label the two equations as the following x 2 2y = 9 y = x 3 Equation 2 can be substituted into equation 1, giving x 2 2( x 3 ) = 9Expanding the brackets and subtracting 9 from both sides means equation 1 becomes x 2 2x 3 = 0Then we can factorise this to create (x 3)(x 1) = 0Which means x = 3, and x = 1 Substituting these values into equation 2 gives usy = 0 and y = 4Substituting x = (4 2y)/3 in equation (1), we obtain 8(4 2y)/3 5y = 9 (32 16 y 15 y)/3 = 9 32 y = 27 y = 32 27 y = 5 x = (4 2 × 5)/3 x = 6/3 x = 2 Hence, x = 2, y = 5 Again, by crossmultiplication method 8x 5y = 9 3x 2y = 4 8x 5 y 9 = 0 3x 2 y 4 = 0 a1 = 8, b1 = 5, c1 = 9 a2 = 3, b2 = 2, c2 = 4Avail 25% off on study pack Avail Offer
Cross Multiplication Method calculator Solve linear equation 7y2x11=0 and 3xy5=0 using Cross Multiplication Method online We use cookies to improve your experience on our site and to show you relevant advertising By browsing this website, you agree to our use of cookies 5 3x y = 3 and 7x 2y = 6 2x y = 11 and 5x 4y = 1Solving Linear Equations by Cross Multiplication Method Here is an example Suppose that we have to solve the following pair of equations 2x 3y−11 = 0 3x 2y−9 = 0 2 x 3 y − 11 = 0 3 x 2 y − 9 = 0 Our solution equality will be of the following form, where we have to figure out the question marks Solve the system of equations by using the method of cross multiplication x/6 y/15 – 4 = 0, x/3 y/12 – 19/4 = 0 asked Jun 23 in Linear Equations by Hailley ( 334k points) linear equations in two variables




R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 4




Solutions Manual For Beginning Algebra 7th Edition By Martin Gay By Cndps109 Issuu
Just by inspection, and assuming integers, 2^3 3^2 = = 17 But if you want to go through the algebra, using the fact that 2^2=4 and 3^1=3, we have 2^x 3^y = 17 4*2^x 3*3^y = 5 Now, if you let u=2^x and v=3^y, we have u v = 17 4u 3v = 5 and again we have u=8, v=9Solved Expert Answer to 3 x 2 y = 2 x ?Unlock StepbyStep (x^2y^21)^3x^2y^3=0 Extended Keyboard Examples x 2 2y 3 1 x y 3 3 Mathematics TopperLearningcom gl2kl500 Starting early can help you score better! So, the solution of the given pair of linear equations is x = 2, y = 5 II By Crossmultiplication method Let us write the given pair of linear equations is 8x 5y – 9 = 0 (3) 3x 2y – 4 = 0 (4) To solve the equations (3) and (4) by crossmultiplication method, we draw the diagram below Hence, the required solution of the given



Solve The Following Pair Of Linear Equations By The Substitution And Cross Multiplication Methods 8x 5y 9 3x 2y 4 Zigya



Mfm2p
Steps for Solving Linear Equation x = 2 y 5 x = 2 y − 5 Swap sides so that all variable terms are on the left hand side Swap sides so that all variable terms are on the left hand side 2y5=x 2 y − 5 = x Add 5 to both sides Add 5 to both sides x = 4, y = 1 WARNING!Graph y=2(x3)^24 Find the properties of the given parabola Tap for more steps Use the vertex form, , to determine the values of , , and Since the value of is positive, the parabola opens up Opens Up Find the vertex Find , the distance from the vertex to the focus Tap for more steps
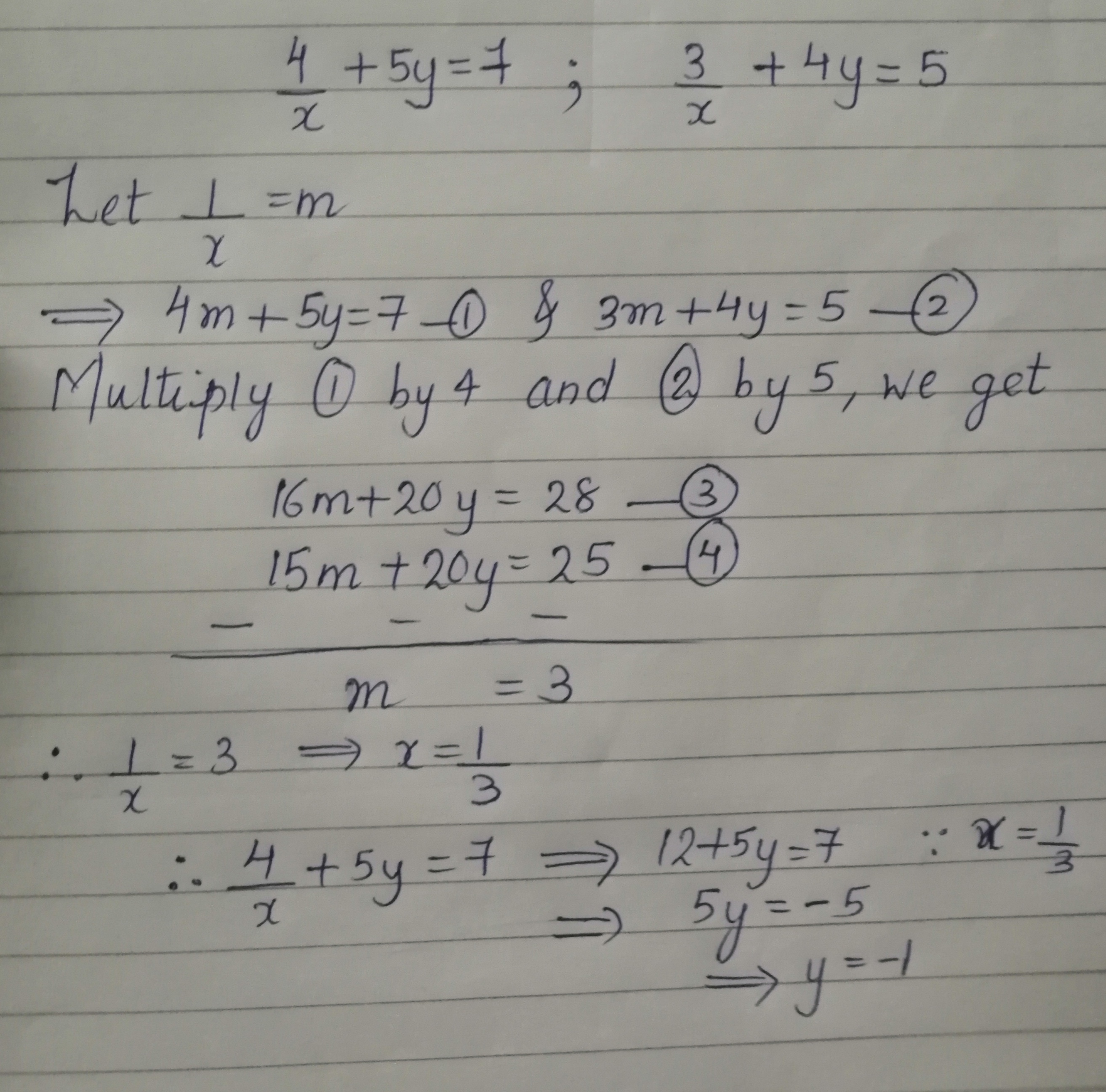



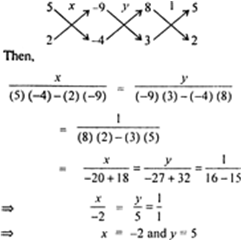
4 X 5y 7 3 X 4y 5 Mathematics Topperlearning Com Eyz2xh55




Solve This By Cross Multiplication Method 2 Ax By A 4b 0 2 Bx Ay B 4a 0 Mathematics Topperlearning Com K2zyk5cc
X = 1/2, y = 1/3 Hence the solution is (1/2, 1/3) Question 2 Akshaya has 2 rupee coins and 5 rupee coins in her purse If in all she has 80 coins totalling ₹ 2, how many coins of each kind does she have Solution Let "x" and "y" number of 2 rupee and 5 rupee coins respectively x y3x 4y 65 =0 asked in Mathematics by sforrest072 ( 128k points) pair of linear equations in two variables`x y/2 = 4` (i) `x/3 2y = 5` (ii) From (i), we get `(2x y)/2 = 4` 2x y = 8 y = 8 2x From (ii), we get x 6y = 15 (iii) Substituting y = 8 2x in (iii), we get x 6(8 2x) = 15 `=> x 48 12x = 15` => 11x = 15 48 => 11x = 33 `=> x = (33)/(11) = 3` Putting x = 3 in y = 8 2x we get y = 8 2 x 3 = 8 6 = 2 y = 2



Solve The System Of Equations By Using The Method Of Cross Multiplication X 6 Y 15 4 X 3 Y 12 19 4 Sarthaks Econnect Largest Online Education Community




Selina Chapter 6 Linear Equations Including Problems Icse Solutions Class 9 Maths
Therefore, the required solution set for the given simultaneous equations is x = 2/5, y = 3/5 Example 2 Solve the equations 2x – y – 3 = 0, 3x 2y – 8 = 0 by using the comparison method?54 Factoring x 4 3x 3 y 4x 2 y 2 3x 2 y 3xy 2 5y 2 Thoughtfully split the expression at hand into groups, each group having two terms Group 1 4x 2 y 2 3xy 2To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW Solve by cross multiplication `x2y1=0 `, `2x3y12=0`




Class Ten Maths Ncert Chapter 3 Solutions Freeguru Helpline



Systems Of Linear Equations
X 2y = 5 by cross multiplication methodThere Are Actually 4 methods of solving this We have, 2x 3y = 11(i) and, 5x 2y = 18(ii) i) Elimination Method First choose which variable you want to eliminate I'm going with y So, Multiply the eq(i) with 2 first It will turn into, 4x 6y = 22(iii) Now, Multiply the eq(ii) with 3PreAlgebra Solve for x 2yx=3 2y − x = 3 2 y x = 3 Subtract 2y 2 y from both sides of the equation −x = 3 −2y x = 3 2 y Multiply each term in −x = 3−2y x = 3 2 y by −1 1 Tap for more steps Multiply each term in − x = 3 − 2 y x = 3 2 y by − 1 1



Solve The Following Systems Of Equations 1 2 X 2y 5 3 3x 2y 3 2 5 4 X 2y 3 5 3x 2y 61 60 Sarthaks Econnect Largest Online Education Community




123a Ppt All 2
Solve the linear equations x y = 5, x – y = 3 by using the cross multiplication method? If 2x y = 23 and 4x y = 19, then find the values of 5y – 2x and y/x 2 asked in Class X Maths by saurav24 Expert ( 14k points) pair of linear equations in two variables Solve using cross multiplication method xy=7 and 2x3y=11 Answers 2 Get Other questions on the subject Math Math, 1000, malikfaiz24 If x=2 ,y=9 and z=8 then 8x3y√64z Answers 2 continue Math, 1100, arpita734 Ineed to demostrate this trigonometric identities urgent!




Multiply 5 X Y X Y 5




Multiply 5 X Y X Y 5
x = 2 and, = 1 y = 5 Hence, the required solution is x = 2 and y = 5 Question 4 Form the pair of linear equations in the following problems and find their solutions (if they exist) by any algebraic method (i) A part of monthly hostel charges is fixed and the remaining depends on the number of days one has taken food in the mess Cross Multiplication Method Examples Example 1 Solve the following system of equations by crossmultiplication method 2x 3y 8 = 0 4x 5y 14 = 0 Sol The given system of equations is 2x 3y 8 = 0 4x 5y 14 = 0 By crossmultiplication, we get Question 3 Below is the picture of the question i need help with, Its a maths question 15 Find the value of 'x'on the curve y = x² – 3x 4 where slope of tangent to the curve is 1a




0 4x 0 3y 1 7 0 7x 0 2y 0 8 7 Y 3 2 X 2 14 4 Y 2 3 X 3 2 X Y 2 4 X 3 2y 5 Solve This In Two Min From Substitution Elimination And Cross Multiplication Method Edurev Class 10 Question



Solve The Following Systems Of Equations 3 X Y 2 X Y 2 9 X Y 4 X Y 1 Sarthaks Econnect Largest Online Education Community
2xy =6 , xy =2 by cross multiplication method pauline mixed 032 l of syrup with 12 times as much water to make orange squash then, she pouring the remaining orange quash equally into 4 bottlesSteps for Solving Linear Equation x2y=4 x − 2 y = 4 Subtract x from both sides Subtract x from both sides 2y=4x − 2 y = 4 − x Divide both sides by 2 Divide both sides by − 2 Correct answers 3 question Solve for x and y 2x – 3y = 4 ;
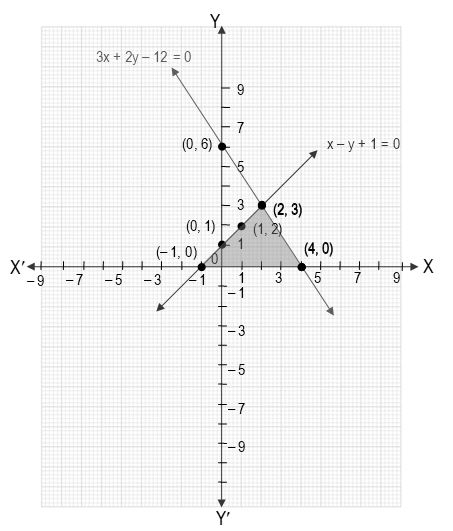



Pair Of Linear Equations In Two Variables




Solve By Reducing Them To A Pair Of Linear Equations 10 X Y 2 X Y 4 15 X Y 5 X Y 2 Youtube
Use the Substitution method to solve the system of equations x y = 4 x y = 2 x y = 4 x y = 2 In the second equation, x= y2 Putting that in the first (y2) y= 4 subtract two from each side, then divide each side by two to get y Then, put mathsSolution Given system of linear equations are x y = 5 x – y = 3 On transposition, we get x y – 5 = 0 x – y – 3 = 0 Writing the coefficient in the following way, we get By crossmultiplication method Ex 35 Class 10 Maths Question 1 Which of the following pairs of linear equations has unique solution, no solution or infinitely many solutions In case there is unique solution, find it by using crossmultiplication method (i) x – 3y – 3 = 0, 3x – 9y – 2 = 0 (ii) 2x y = 5, 3x 2y = 8 (iii) 3x – 5y = , 6x – 10y = 40




X 6 Y 15 4 X 3 Y 12 19 4 Solve Using Cross Multiplication Method Brainly In




Ex 3 6 1 V And Vi 7x 2y Xy 5 8x 7y Xy 15
Solve the equations using the cross multiplication method 3x 2y = 10 and 4x − 2y = 4 Get the answer to this question and access other important questions, only at BYJU'SBy applying the value of x = 4 in (1), we get 4 2y = 7 2y = 7 – 4 2 y = 3 y = 3/2 Hence the solution is (4, 3/2) Example Problem of Solving System of Linear Equations By Cross Multiplication Method Example Solve the following system of linear equations by cross multiplication method 3x4y = 24, x11y = 47 Solution 3x4y24 = 0In Maths, cross multiplication method is used to solve linear equation in two variables This is the simplest method and gives the accurate value of the variables Cross multiplication is only applicable when we have a pair of linear equations in two variables Let us suppose that a1x b1y c1 = 0 and a2x b2x c2 = 0 are the two equations which has to be solved
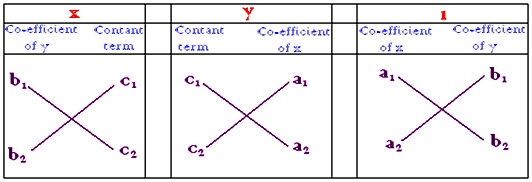



Cross Multiplication Method Formula For Cross Multiplication Linear Equations




Solve The Following Pair Of Equations By Cross Multiplication Method 2x 5y 4 3x 8y 5
Given equation are 8x 5y = 9 and 3x 2y = 4 Comparing with a 1 x b 1 y c 1 = 0 and a 2 x b 2 y c 2 = 0, We have a 1 = 8, b 1 = 5, c 1 = 9 and a 2 = 3, b 2 = 2, c 2 = 4 Now, x = ` b_1c_2 b_2c_1 / a_1b_2 a_2b_1 and y = c_1a_2 c_2a_1 / a_1b_2 a_2b_1 `Solve each of the following systems of equations by the method of crossmultiplication 2x y 35=0;Hence the solution is #x=1,y=1# Substitution Method From Eqn 2 we have #x=32y#> Eqn 3 Substitute in Eqn 1 # 6*(32y)4y = 2# #1812y4y=2# #16y=218# #16y = 16# #y=1# Use in eqn 3 #x = 321# #x=1# So we get #x=1,y=1#




Mathsmentor Answers Page 32 Ask Truemaths



Solve By Using Cross Multiplication Method 3x 4y 10 And 2x 2y 2 Class 10 Brainly In
3x 2y = 4 (ii) (I) By substitution method From equation (ii), we have 2y = 4 3x Substitute this value ofy in equation (i), we get Substituting this value of x in equation (iii), we get So, the solution of the given pair of linear equations is x = 2,y = 5 (II) By crossmultiplication method Let us write the given pair of linearAre solved by group of students and teacher of Class 10, which is also the largest student community of Class 10 Ex 35, 3 (Substitution method) Solve the following pair of linear equations by the substitution and crossmultiplication methods 8x 5y = 9 3x 2y = 4 8x 5y = 9 3x 2y = 4 From (1) 8x 5y = 9 8x = 9 – 5y x = ((9 − 5𝑦))/8 Putting value of x in (2) 3x 2y = 4 3 (((9




Multiply 5 X Y X Y 5
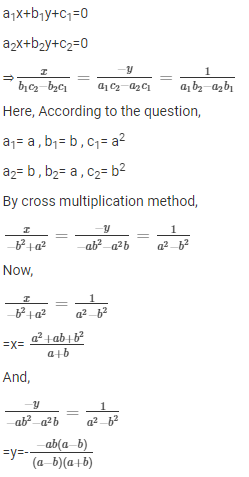



Rd Sharma Solutions For Class 10 Maths Chapter 3 Pair Of Linear Equations In Two Variables Free Study Material Cbse Sample Papers Books Studyguide360
Solve a system of two linear equations in two unknowns (variables) Use the (GaussJordan) elimination method to eliminate one variable linear system x 2 y = 5 3 x − y = 1 Eliminate the variable y by scaling equation (2) by 2 Then, subtract the new equations, (1) (2a) to get variable x alone x 2 y = 5The given simulattaneous equations are 4xy =3 X2y =3 4x3y3=0 (1) x2y3=0 (2) Fo calculating values of xand y of the given equations cross multiplication mehod is used The method name it self indicates cross multiplication Cross multiplicat Transcript Example 7 Solve the following pair of equations by substitution method 7x – 15y = 2 x 2y = 3 7x – 15y = 2 x 2y = 3 From (1) 7x – 15y = 2 7x = 2 15y x = (𝟐 𝟏𝟓𝒚)/𝟕 Substituting the value of x in (2) x 2y = 3 (2 15𝑦)/7 2𝑦=3 Multiplying both sides by 7 7 × ((2 15𝑦)/7) 7×2𝑦=7×3 (2 15y) 14y = 21 15y 14y = 21 – 2 29y = 21 – 2




Coss Multiplication Method For Solving Linear Equations Ncert 10




Solve The Following Equation Using Cross Multiplication Method 7x 9y 19 0 And 4x 5y 21 0 Brainly In
If the linear equation in two variables 2x –y = 2, 3y –4x = 2and px–3y = 2are concurrent, then find the value of p If ܽa b = 35 and a − b =Solve the simultaneous equations x^2 2y=9, yx=3 Use the method of substitution to answer this question Step 1 Rearrange one of the equations to find x or y yx=3 y=x3 Step 2 Substitute your y into the first equation x 2 2y=9 x 2 2 (x3)=9 Step 3 Expand the brackets and rearrange to form a quadratic equation




7 Y 3 2 X 2 14 4 Y 2 3 X 3 2 Youtube




14 2 Limits And Continuity
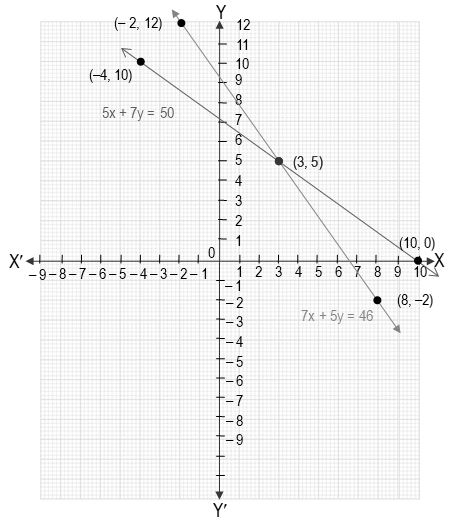



Pair Of Linear Equations In Two Variables




How To Solve 2 X 3 Y 7 1 X 4 Y 2 Where X And Y Is Not Equal To 0 By Cross Multiplication Method Quora
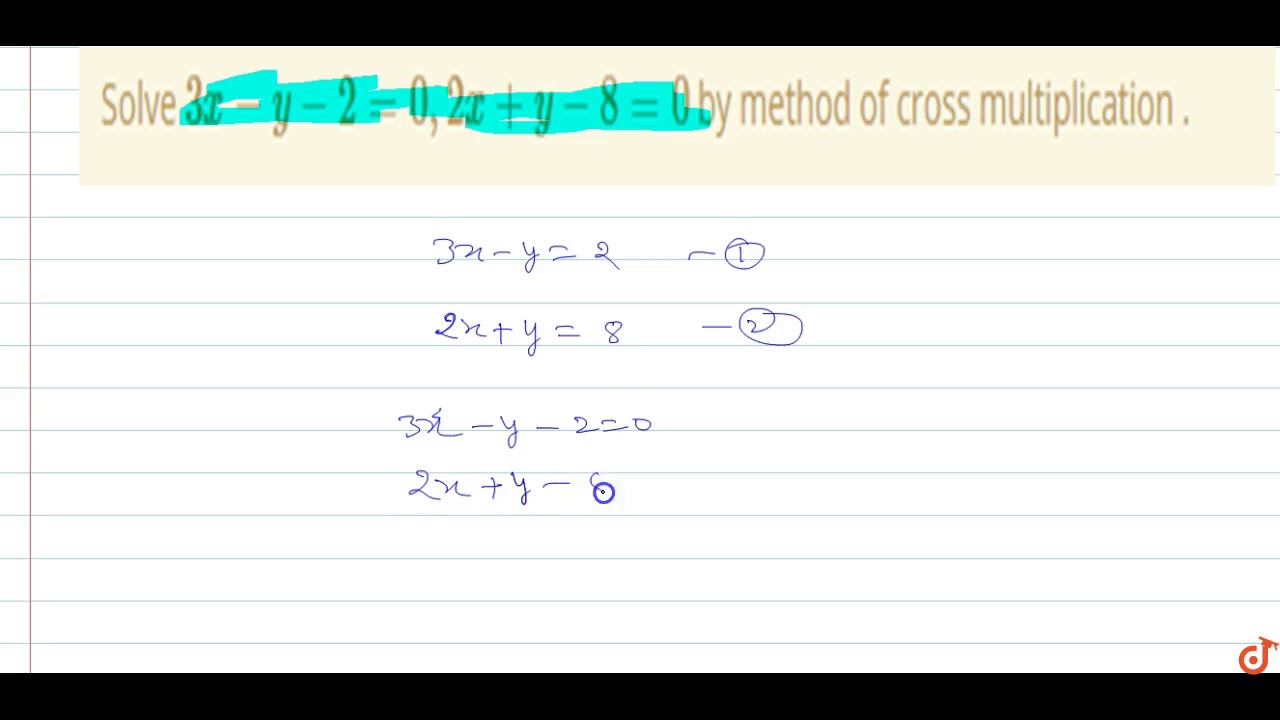



Solve 3x Y 2 0 2x Y 8 0 By Method Of Cross Multiplication Youtube




Coss Multiplication Method For Solving Linear Equations Ncert 10




Coss Multiplication Method For Solving Linear Equations Ncert 10




Maths Cross Multiplication Method Pair Of Linear Equations In Two Variables Part 4 English Youtube



3




Ex 3 5 3 Solve By Substitution And Cross Multiplication Teachoo



Solve The Following Systems Of Equations 10 X Y 2 X Y 4 15 X Y 5 X Y 2 Sarthaks Econnect Largest Online Education Community




123a Ppt All 2




Chapter 5 Simultaneous Linear Equations Ml Aggarwal Icse Solutions For Class 9 Maths




Solve The Following Pair Of Linear Equations By The Substitution And Cross Multiplication Methods 8x 5y 9 3x 2y 4



Multiply 5 X Y X Y 5



10 X Y 2 X Y 4 And 15 X Y 5 X Y 2 P S 1 4 Q2 Linear Equation In Two Variables Youtube




Ex 3 5 3 Solve By Substitution And Cross Multiplication Teachoo




Selina Chapter 6 Linear Equations Including Problems Icse Solutions Class 9 Maths




3 Systems Of Linear Equations




Linear Equations In Two Variable Exercise 3 Solutions Edusaint




Example 18 Solve 5 X 1 1 Y 2 2 6 X 1 3 Y 2 1 Examples




Multiply 5 X Y X Y 5




Selina Chapter 6 Linear Equations Including Problems Icse Solutions Class 9 Maths



Q Tbn And9gcs9tgm5jownqcbmmkn Hor7zjt04wxusrmdjwjoes2jikwdevca Usqp Cau



Solve The Following Systems Of Equations 1 2 X 2y 5 3 3x 2y 3 2 5 4 X 2y 3 5 3x 2y 61 60 Sarthaks Econnect Largest Online Education Community




123a Ppt All 2



Amitbajajcrpf Files Wordpress Com 12 06 Ch1 Linear Equation In Two Variables Main Pdf




Cross Multiplication Method For Solving Equations A Plus Topper




Ch1 Linear Equation In Two Variables




Coss Multiplication Method For Solving Linear Equations Ncert 10




What Is 4x Y X 2y 3 By Cross Multiplication Method Quora



Q Tbn And9gcqxnk Lpfjle Erogd0wsraw D67yjyrnkghuofquiwt4u Rzfp Usqp Cau



Solve The Following Systems Of Equations X Y 2 4 X 3 2y 5 Sarthaks Econnect Largest Online Education Community




Solve 3x 2y 12 And 4x Y 5 Using Cross Multiplication Method Brainly In




Ch1 Linear Equation In Two Variables




無料ダウンロード 3x 2y5 X5 Y




Coss Multiplication Method For Solving Linear Equations Ncert 10



How To Solve 1 X 1 Y 7 2 X 3 Y 17 Where X And Y Is Not Equal To 0 By Cross Multiplication Method Quora




7lsnwr9avofjvm




Ex 3 5 3 Solve By Substitution And Cross Multiplication Teachoo




X 2y 2x 3y 7solve By Cross Multiplication Method Brainly In




Which Of The Following Pairs Of Linear Equations Has Unique Solution No Solution Or Infinitely Many Solutions I X 3y 3 0 3x 9y 2 0




Solve The Following Pair Of Linear Equation Bycross Multiplication Method X 2y 2 X 3y 7




Ch1 Linear Equation In Two Variables



How To Solve 1 X 1 Y 7 2 X 3 Y 17 Where X And Y Is Not Equal To 0 By Cross Multiplication Method Quora




無料ダウンロード 3x 2y5 X5 Y




Cross Multiplication Method For Solving Equations A Plus Topper




How To Solve By Cross Multiplication For X By 2 Ax By A 4b 0 2 Bx Ay B 4a 0 Quora
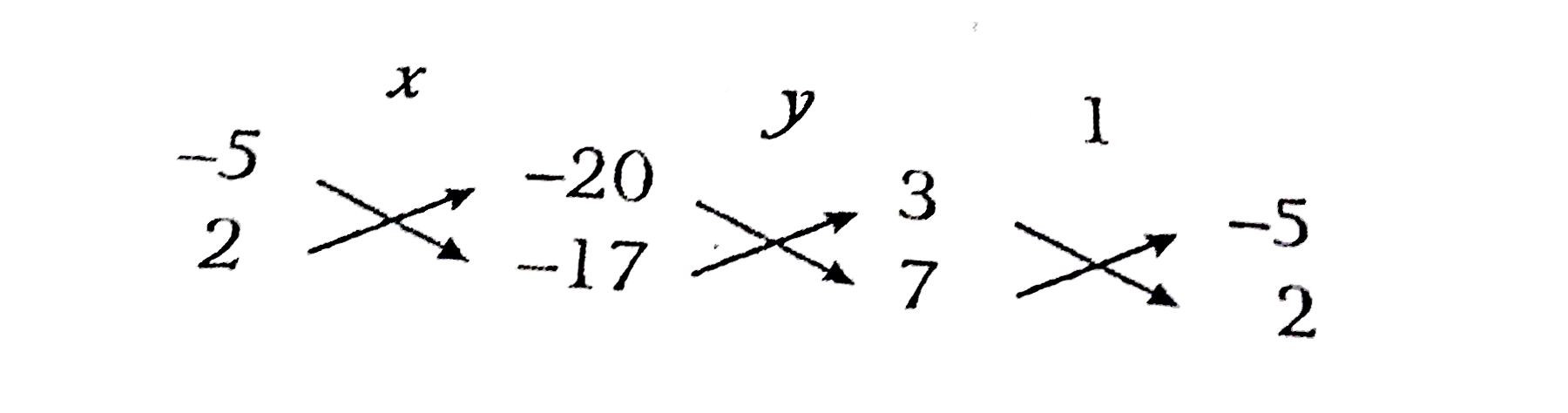



क र स ग ण पद धत द व र सम करण क न म न प रण ल क हल कर 3x



How To Solve The Following Simultaneous Equations By Elimination Method A 2x 3y 12 X Y 1 B 3x Y 10 C X 3y 1 3x 2y 4 0 D 5 Quora




Rd Sharma Solutions For Class 10 Updated For 21 22 Chapter 3 Pair Of Linear Equations In Two Variables




Systems Of Equations With Elimination X 2y 6 4x 2y 14 Video Khan Academy




Cross Multiplication Method For Solving Equations A Plus Topper




In The Following System Of Equation Determine Whether The System Has A Unique Solution No Solution Or Infinitely Many Solution In Case There Is A Unique Solution Find It 2x 3y




हल क ज ए 2x Y 5 3x 2y 8 Youtube




Solve The Pair Of Linear Equations By Cross Multiplication Method 2 2x Y 5 3 X 3y 1 0 Brainly In




Solve The Following System Of Equations By Method Of Cross Multiplication 2x Y 6 X Y 2




無料ダウンロード 3x 2y5 X5 Y




Ex 3 6 1 V And Vi 7x 2y Xy 5 8x 7y Xy 15




Solve The Pair Of Linear Equation By Cross Multiplication Method 5x 4y 4 0 X 12y 0 Brainly In




Solve By Cross Multipication 3x 2y 11 2x 3y 4




123a Ppt All 2




R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 4



Solve The Following Systems Of Equations X Y 2 4 X 3 2y 5 Sarthaks Econnect Largest Online Education Community




Solving Linear Equations By Cross Multiplication Method X 2y 2 X 3y 7 Brainly In




Coss Multiplication Method For Solving Linear Equations Ncert 10



6x 3y 6xy 2x 4y 5xy



Linear Systems With Multiplication Algebra Socratic




Solve X Y 7 And 3x 2y 11




How To Solve By Cross Multiplication For X By 2 Ax By A 4b 0 2 Bx Ay B 4a 0 Quora



Systems Of Linear Equations



Solve The System Of Equations By Using The Method Of Cross Multiplication X 6 Y 15 4 0 X 3 Y 12 19 4 0 Sarthaks Econnect Largest Online Education Community




क र स ग ण पद धत द व र सम करण क न म न प रण ल क हल कर 3x
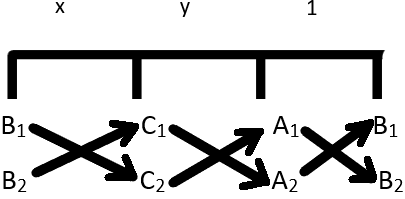



Method Of Cross Multiplication Solve By Method Of Cross Multiplication




X 2 2y 3 1 And X Y 3 3 Find X And Y Values Using Elimination And Substitution Method Youtube



Pair Of Linear Equations In Two Variables



0 件のコメント:
コメントを投稿