平行線の定義・・・錯角の等しい2直線は平行である。 この定義から次の性質、条件が導ける。 平行線の性質 2つの直線に1つの直線が交わるとき、 2つの直線が 平行なら錯角は等しい 。 2つの直線が 平行なら同位角は等しい 。 平行線になる条件 定義 15 において平行線は以下のように導入される「同じ向きを持つが一つの同じ直線の部分となっていない直線を平行線と呼ぶ」 。 オーガスタス・ド・モルガン はこの教科書を批評して、主にこの定義およびウィルソンが平行線に関する内容を証明するのに用いた方法に基づいて誤りで (1)一方向の平行度 ・公差域の定義(jis原文、以下同様) その方向に垂直でデータム直線(l d )に平行な幾何学的平行2平面でその直線形体(l

台形と平行四辺形の定義 ちがい 小岩 個別指導 元小学校教師が教える個別指導塾 できる子ども育成塾 小岩 篠崎の小学生専門 国語と算数の苦手を克服
平行 の 定義
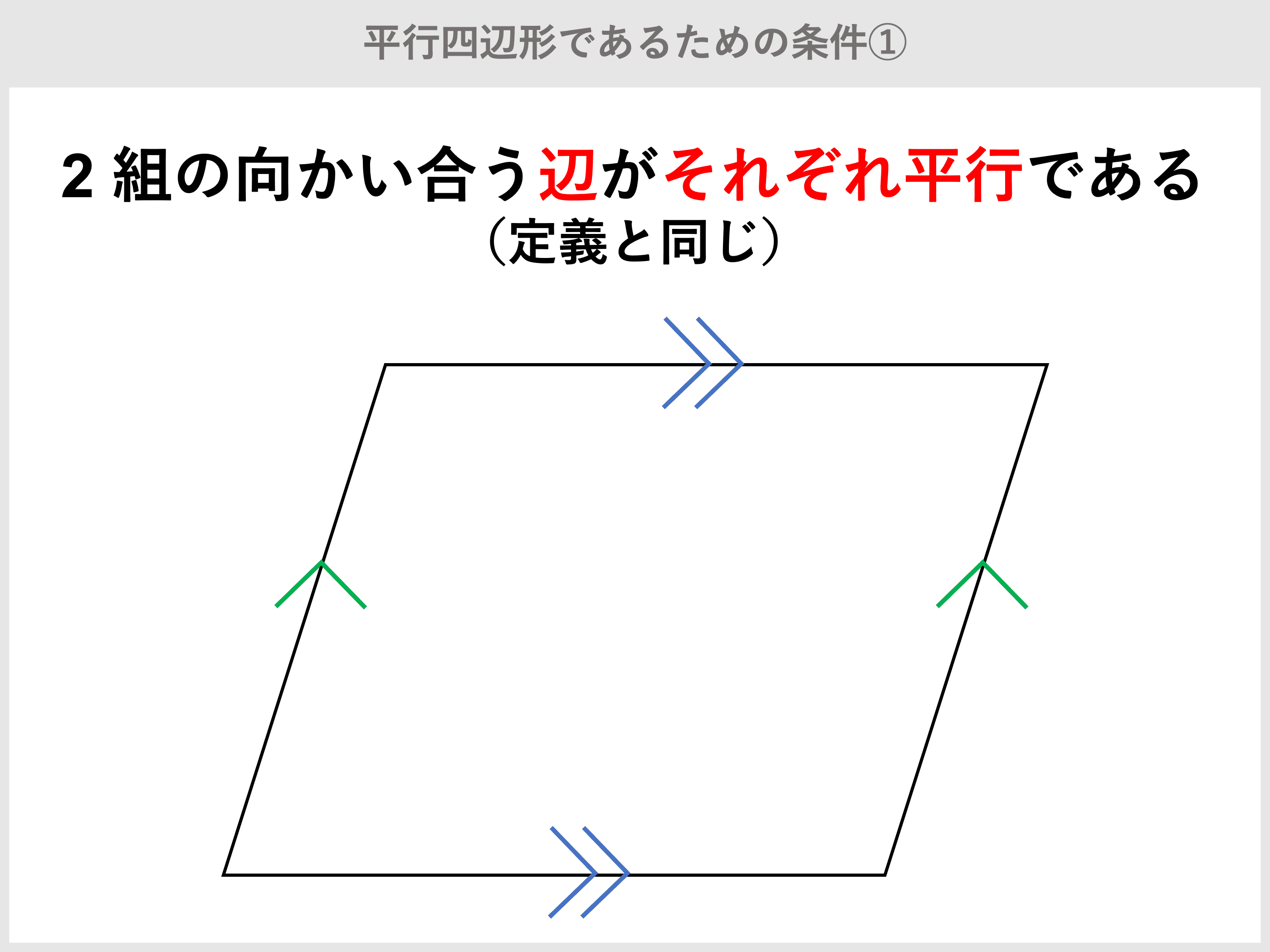
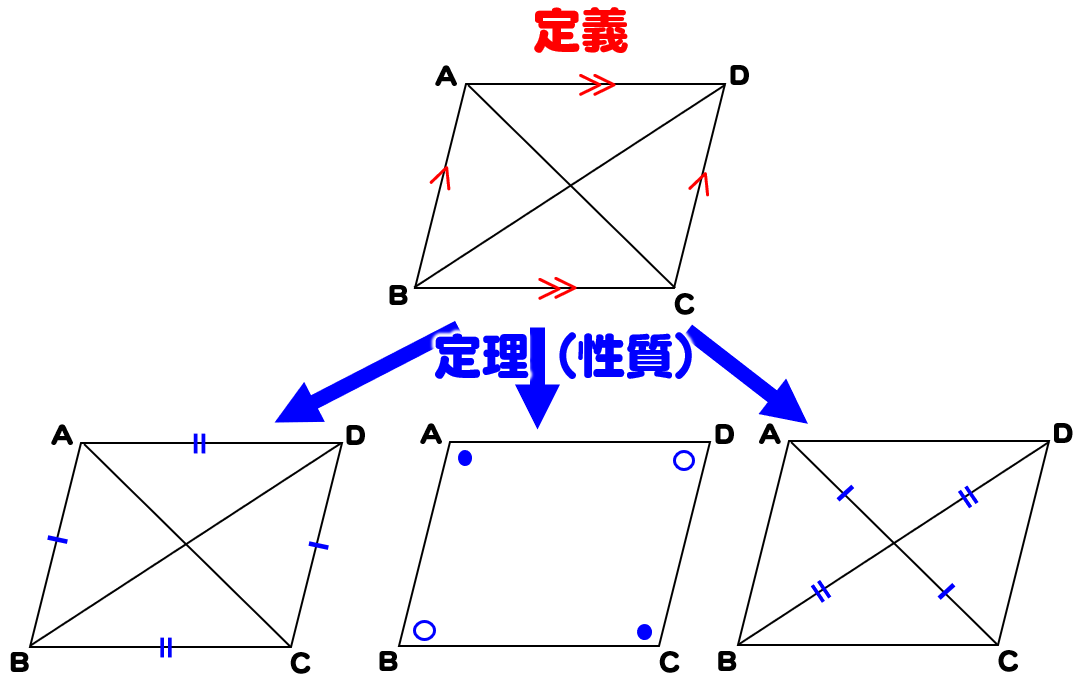
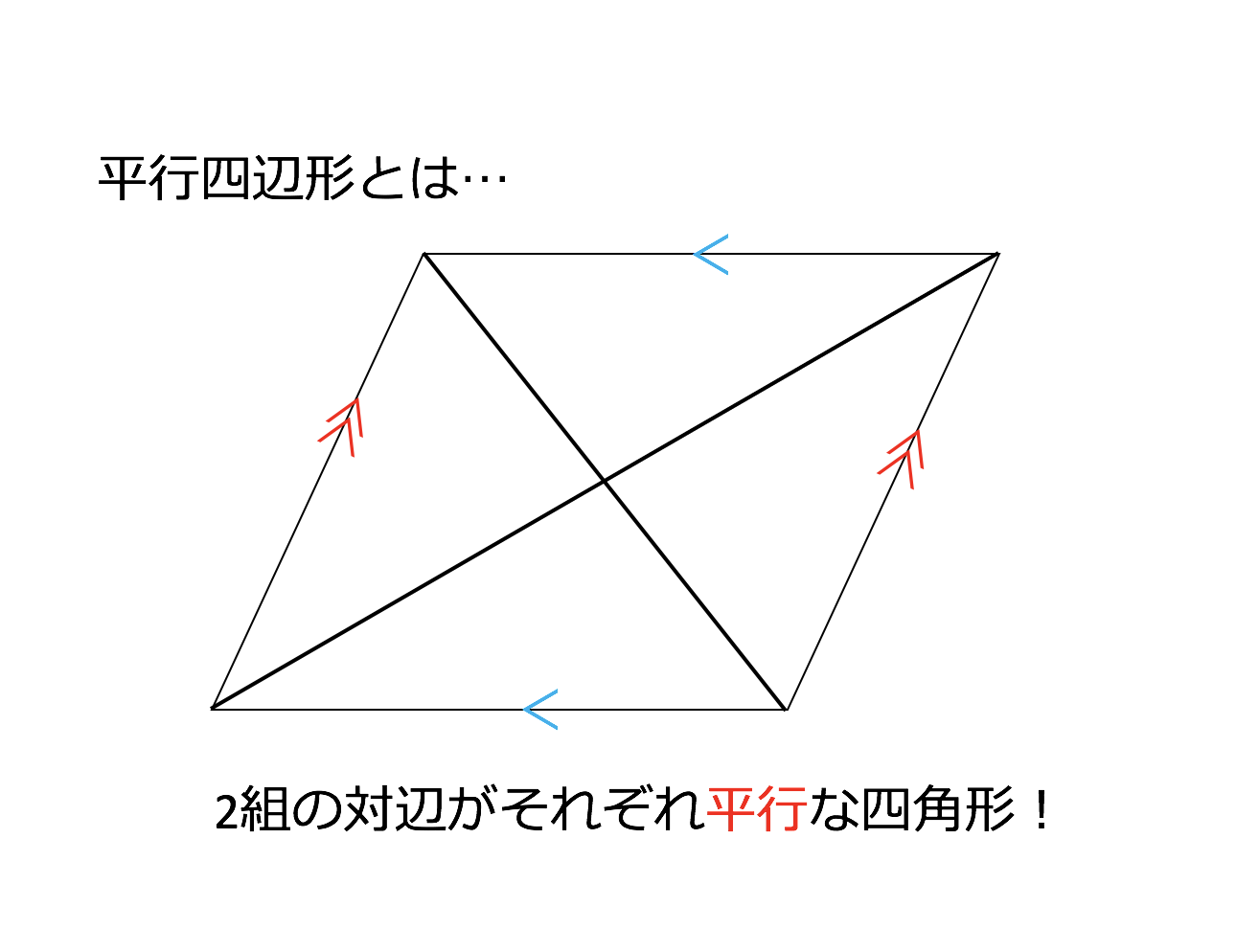
平行 の 定義- 平行四辺形とは、 \(\bf{2}\) 組の向かい合う辺がそれぞれ平行な四角形 のことです。 まずはこの定義をしっかり覚えておきましょう。 平行四辺形の性質(定理)平行四辺形の定義 2組の向かい合う辺が、それぞれ平行な四角形を平行四辺形という。 平行四辺形の性質 内容 (ヒントの図)1 平行四辺形の向かい合う辺は等しい。(証明) 2 平行四辺形の向かい合う角は等しい。(証明) 3 平行四辺形の対角線は、それぞれの中点で交わる。
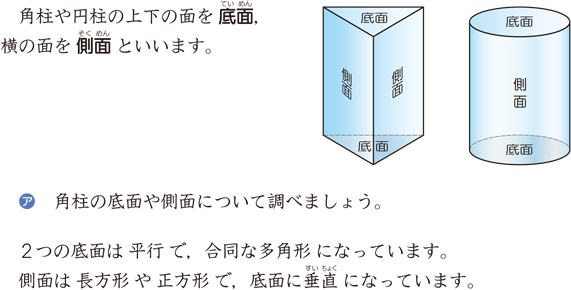



角柱と円柱 算数用語集
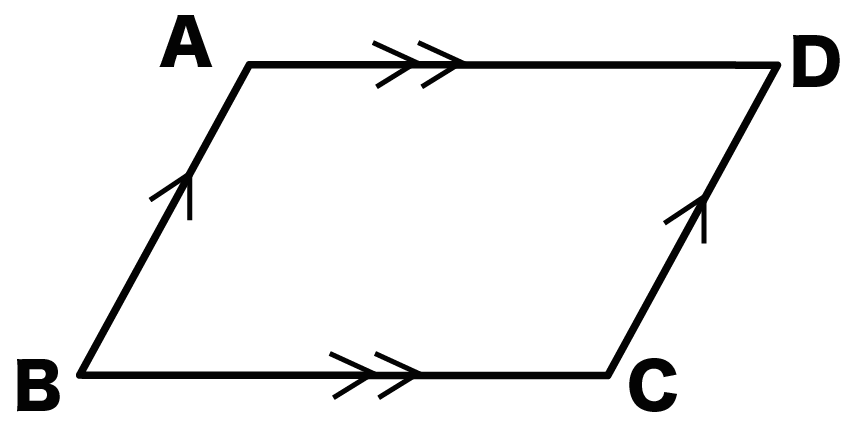
定義 四角形abcdが平行四辺形とは ab∥dc,ad∥bc を満たす四角形である. 四角形で,向かい合う辺を 対辺 ,向かいあう角を 対角 といいます. 現時点では,平行四辺形では2組の対辺がそれぞれ平行であるしか使えません. やりとりしている際に「平行の定義」が問題になった。 「積分定数」氏は 「私は、平面の平行線は『どこまで行っても離れたり近づいたりしない2本の直線』というイメージで 捉えていましたが、『教科書の定義』は違います。 」 と述べて、啓林館のサイト https//wwwshinkokeirincojp/keirinkan/sansu/WebHelp/04/page4_18html にリンクが張ってあった。 そこにある 小学校での 平行 の定義 平行 を教えるときに、一般的な定義である 「対象(直線)がどこまでいっても交わらない状態」と教えた方が分かりやすいと思うのですが、どうして小学校では 「1つの直線に対し垂直な
間違いではありませんが、この図は平行四辺形の一例を示しただけです。 平行四辺形の定義は「 2組の向かい合う辺が、それぞれ平行な四角形 」です。 ですから 正方形も長方形も平行四辺形の仲間であると言えます。日本大百科全書(ニッポニカ) 平行の用語解説 同一の平面上にあって交わらない2直線を平行であるという。2直線が平行のとき、これに別の直線が交わってできる同位角は等しい(図(1))。平行定規 角度定規 測定ツール 長さ約30cm PVCプラスチック製 高精度 目盛り付き 平行ロール定規
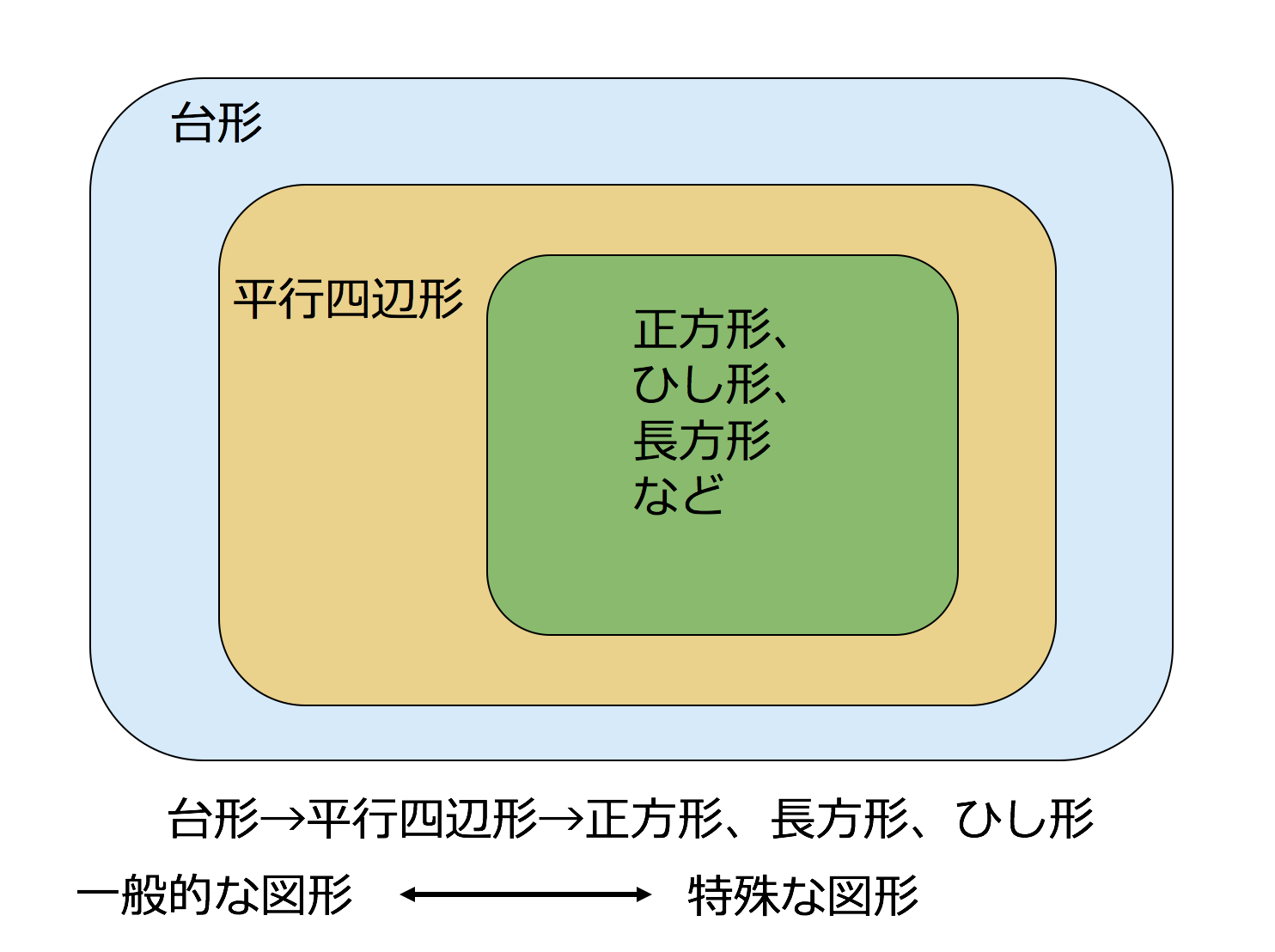
ユークリッド原論をどう読むか(3) 頁末 前 次 目次 ユークリッド原論 第1巻 命題1ー27(錯角と平行) 錯角 もし 1直線が2直線に交わってなす錯角が 互いに等しければ、 この2直線は互いに平行であろう。 直線は、定義1ー4による。図形 定義・定理 まとめ 対頂角 𝟖は等しい 直線の角度 ° 平行線の 同位角 𝟖 は等しい 角形の内角の和 °×(𝒏− ) 平行線の 多角形の外角の和錯角 𝟔は等しい ° 同位角 が等しければ、2直線は平行 〇 合同な図形の対応する線分や角は等し 平行四辺形とは、「 2組の向かい合う辺 (対辺)が、それぞれ平行な四角形 」のことを指します。 また、平行四辺形は 台形 の一種です。 さらに、平行四辺形の中には特別に名前のついている四角形があり、それが 正方形やひし形、長方形 と呼ばれる四角形のことです。 図にまとめたので確認してみてください。 平行四辺形の定義はとても重要なので、次



平行とは コトバンク




平行四辺形の定理や定義 平行四辺形の覚えておきたい性質は4つ 中学や高校の数学の計算問題
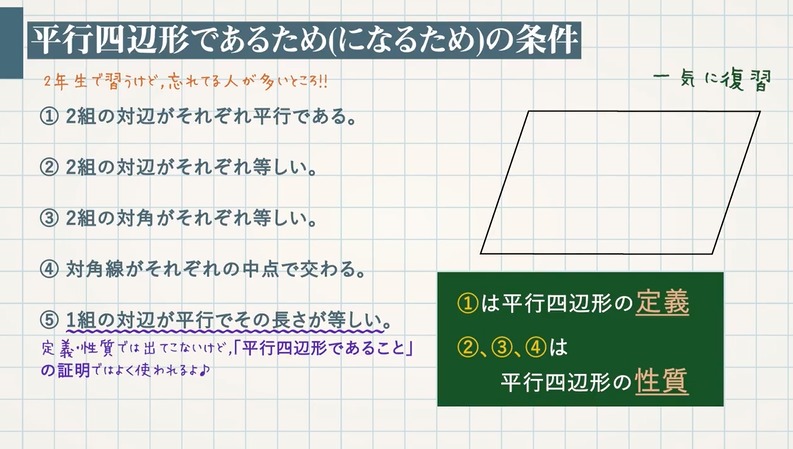
「定義」 :こういうものを平行四辺形と呼ぼう! 「性質」 :平行四辺形と呼ばれるものには 共通してこんなことが言えるね! 「定理」 :性質の中で特に大切なこと! だから証明はいらないよ! こんな感じです。 例えば、コーラ。平行四辺形になるための5つの条件を理解しておく必要がある。 平行四辺形になるための5つの条件は次の通り。 ①2組の向かい合う辺がそれぞれ平行である。(定義) ②2組の向かい合う辺がそれぞれ等しい。 ③2組の向かい合う角がそれぞれ等しい。姿勢偏差の「平行度」とは さまざまな姿勢を指定する幾何公差の中でも姿勢偏差にあたる「平行度」についてご説明します。 平行度は、データムに対して平行であることが求められるときに指示する幾何公差です。 通常であれば、加工によって大幅に平行度がずれることはありませんが、設計上必要な場合に指定します。 たとえば、下記のようなブロックがあり




平行線と角 対頂角 錯角 同位角とは 教遊者




ポストカード 平行線の定義 はれ ときどき くもりあめ Suny Sometimes Cloudy Rainy
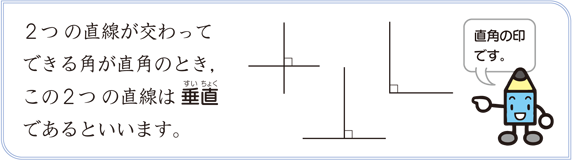
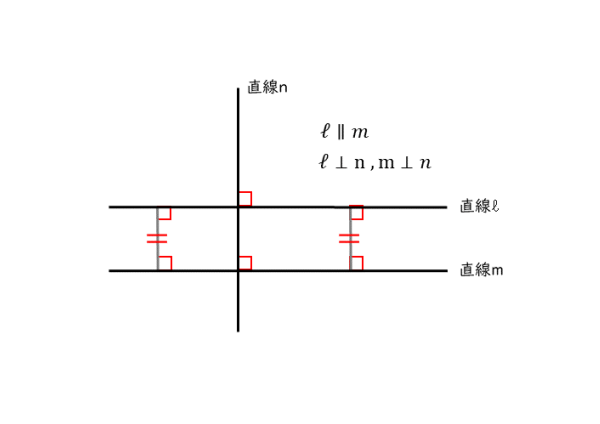
定義と性質 例えば,平行四辺形を学習した児童に「平行四辺形を1つかきなさい」と問いかけると,各自が思い思いに平行四辺形をかき出してきます。 しかし,かかれる平行四辺形は,当然のことながらその大きさも,形も,向きも異なった平行四辺形です。 しかし,こうした個々の平行四辺形をいくらかき出しても,平行四辺形の概念が確立したとは言い切れませ⑤ 平行頂げき:歯先円すい母線と相 手歯車の歯底円すい母線は平行 定義:歯すじが直線で円すい頂点に向かっているかさ歯車。 特徴: ① 歯たけ:ℎ=225𝑚 ② 頂げき: =025𝑚 ③ かみあい歯たけ:ℎ=2𝑚 ④ 標準歯車:転位なし 転位なし 転位平面における直線の垂直・平行は,2本の直線の位置関係を表しています。 位置関係ですので,2 本の直線の長さには,全く関係ありません。 位置関係を成立させる条件だけを保っていれば,それで十分です。 その条件として示されてくるのが,垂直の場合であれば,「2つの直線が直角に交わる」ということです。 この条件を満たしさえすれば,2つの直線は常に
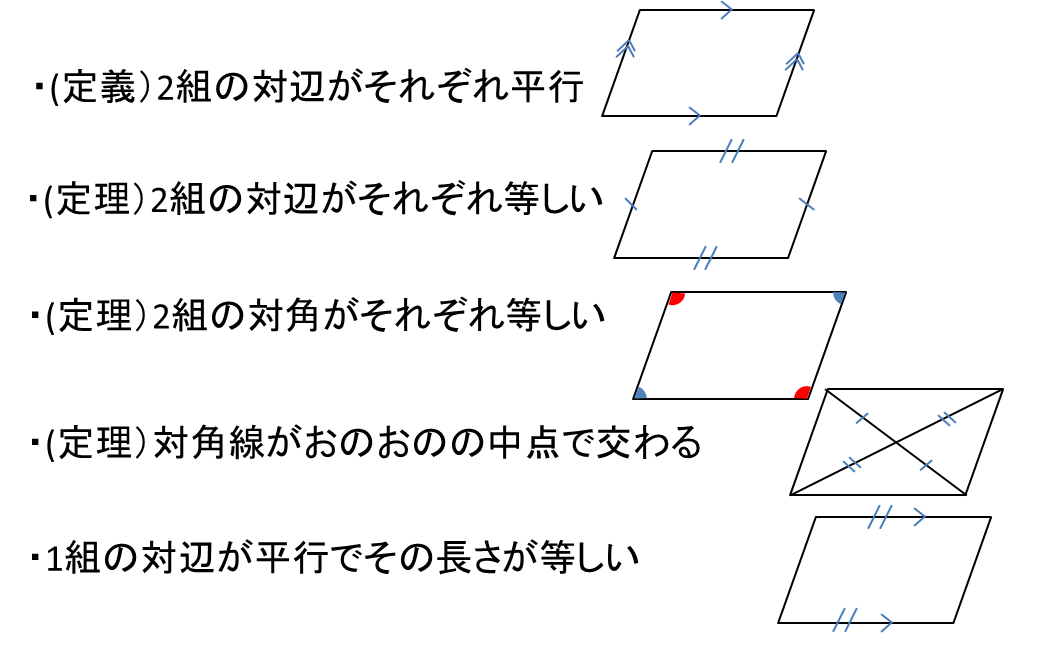



140字で高校受験 数学 平行四辺形の定義 性質 なるための条件 言葉だけでなく図で覚える T Co Amwmvf58n7




平行 Wikipedia
平行軸の定理(Steinerの定理)を求めてみる。 図がきたないとか言わない! 考え方は、質量中心の座標を、(x G, y G, z G)とおいて、そこからhだけ平行移動したところを原点として、その慣性モーメントを求めてあげる。 hだけ平行移動したことから、 となる。 平行度には、以下の種類(用途)があります(「jis b 幾何偏差の定義及び表示 Definitions and designations of geometrical deviations」参照以下、JIS B定義は「こういう四角形を平行四辺形としよう」と決めたことなので、これを証明することはできません。 「なぜ平行四辺形の向かい合う2組の辺は平行なのか?」と問われたら、 「そのような四角形が平行四辺形と定義されているから」 という答えになってしまいます。



1




第4回垂直 平行と四角形 Youtube
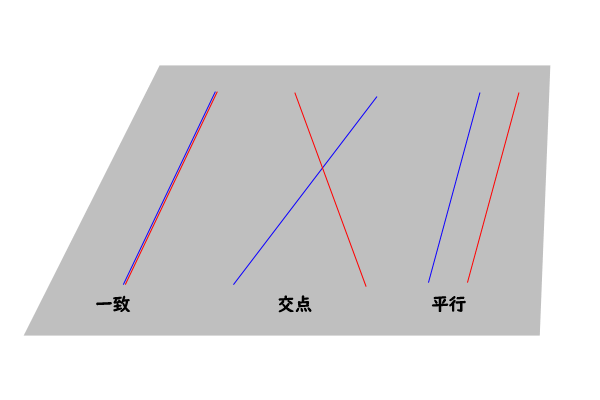
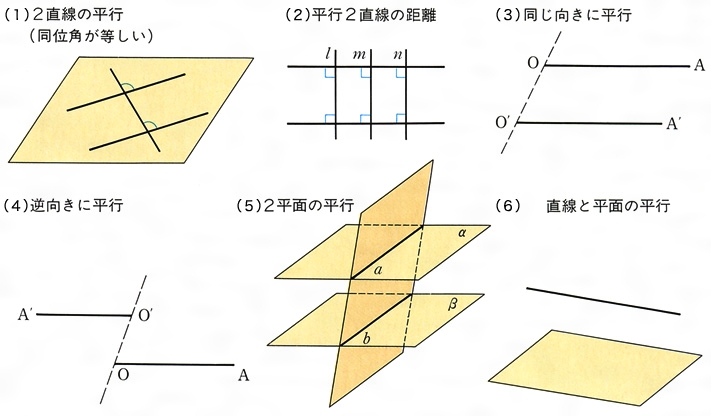
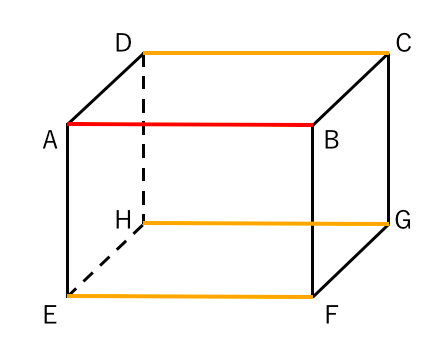
平行線公理へいこうせんこうり ユークリッドの《幾何学原本》にある5番目の公準をいう。 これは〈一直線外の一点を通ってこの直線に平行な直線は一つあり,ただ一つに限る〉と同値。 他の公準より形が複雑なため,他の公理・公準から証明する試みが繰り返されたがすべて失敗。平行な2つの平面P、Qに1つの 平面Rが交わる時、交わりの直 線l、mは1つの平面R上にあっ て交わることがないよね。 つ まり、 l//m ということだね。Q z平行線け 2三角定規合わさい こ直角い 決めらた作図の方法らわず考えた平行四辺形の作図の方法や道具の使い方を説明し、 質問し合いらその整合性を確め活動 70 作図通平行定義 え直平行四辺形定義 関連付け考えこ V {垂直関連付け平行定 義1本直線垂直2本



Corel Designer ヘルプ 投影された描画プレーンをインタラクティブに定義する




平行度 平面度について 竹内型材研究所
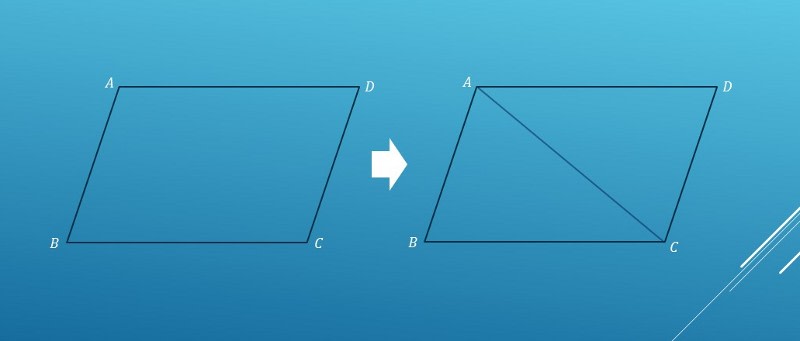
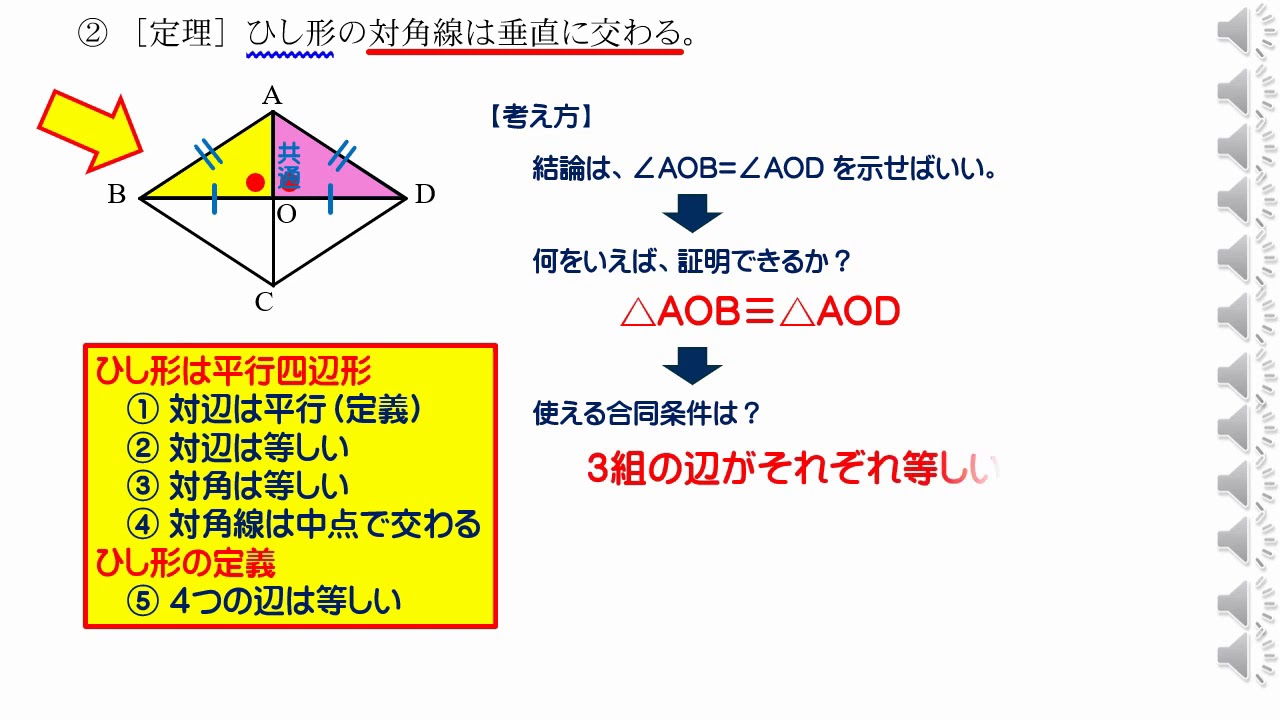
AD//BC(平行線の性質) AC=CA(共通) 3 1,2,3より2辺とその間の角がそれぞれ等しいので1.語句の定義が難しい 啓林館算数教科書4年生「垂直と平行」は、単元冒頭で道路の描かれた絵地図をもとに、子供たちが道路の垂直・平行の関係を探し出すという流れで始まります。 「垂直と平行」あるいは「垂直と直角」「直線と線分」交わる」などは、よくよく考えてみると大人 ア 直線の平行や垂直の関係について理解すること。 イ 平行四辺形、ひし形、台形について知ること。 図形については、第2学年で「長方形と正方形、直角三角形」、第3学年では「二等辺三角形と正三角形」を学習してきている。 これまでの学習は、図形をとらえる視点として、「辺や頂点の数」、「辺の長さ」、「角の大きさ」に着目している。 ここで



垂直と平行 拡大表示は大切 算数4年生の学習指導案 授業案 教材 Edupedia エデュペディア 小学校 学習指導案 授業案 教材




台形と平行四辺形の定義 ちがい 小岩 個別指導 元小学校教師が教える個別指導塾 できる子ども育成塾 小岩 篠崎の小学生専門 国語と算数の苦手を克服
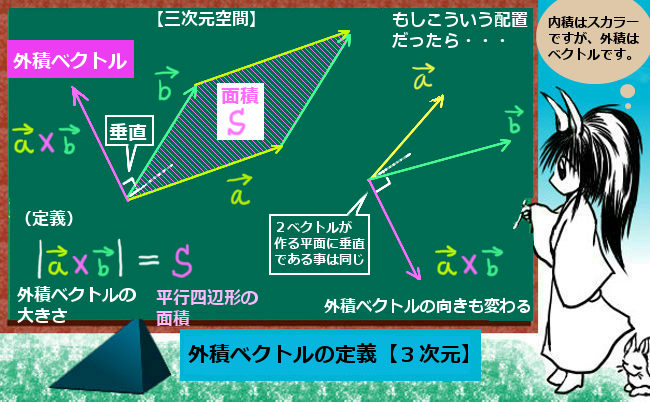
平行四辺形の定義は与えられていないが、 命題1ー34の記述にしたがえば、 向かい合う二組の辺がそれぞれ互いに平行であるというのが 平行四辺形の定義となる。 (以下、定義1ー22の補足2(平行四辺定義できる 特に, 平面のx 軸, y 軸の方向は右手系をなす 右手を左手に入れ換えて左手 系が定義される a b c 2 面積と体積 21 平行四辺形の面積 n 次元ベクトルa,b の作る平行四辺形(右下図) の面積をS とすれば, a,b のなす角をθ (0 ď θ ď π) として,




会津若松ザベリオ学園小学校 算数 垂直と平行と四角形 五十島 真仁教諭




平行四辺形の定義と性質 証明問題の解き方 数学fun




並行と平行の違いとは 併行の意味や使い分けも解説



定義 定理 公式 中学数学基本事項 2年生 平行線と多角形 Mathrao




定義と定理 12月 年 光が丘中学校 ブログ 光が丘中学校
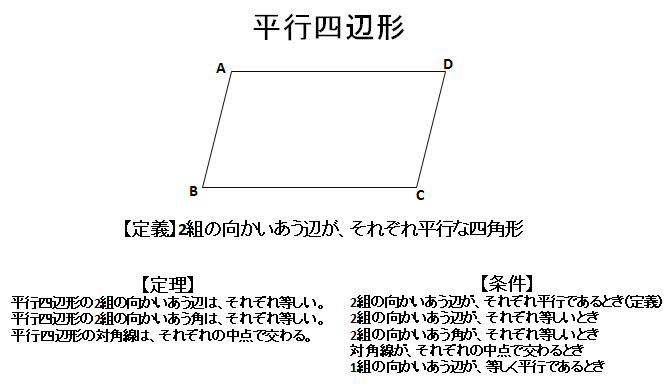



中2数学 平行四辺形の性質と証明の要点まとめノート 中学生勉強サイトあかね先生




平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ




小学4年生の算数 台形 平行四辺形 ひし形 対角線 問題プリント ちびむすドリル 小学生



壮大 平行 の 定義




中学校数学 証明のコツ 平行四辺形と錯角 同位角の相互関係を理解する過程で 証明する力を確実に伸ばすことができる自学自習教材



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典



直線の垂直 平行の関係 算数用語集



平行四辺形の定義と性質 証明問題の解き方 数学fun



4年算数 垂直 平行と四角形 1 教え方のポイント



中2数学 平行と合同では 図形の定義は完璧に暗記しておくこと 桜華塾 お役立ちブログ 楽天ブログ



空間における平行な直線の推移関係について 高校数学マスター



平行とは コトバンク



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典




平行四辺形の定義から性質と条件をわかりやすく証明 特に対角線の性質を押さえよう 遊ぶ数学



ベクトルの平行条件 垂直条件とは 内積公式や証明 計算問題 受験辞典




並行 平行 併行 平衡 の意味と違い 社会人の教科書




角柱と円柱 算数用語集




小学校4年生での平行の定義 小学校学習指導要領解説 算数編 は問題が多すぎる 身勝手な主張



図形と方程式 2直線の平行条件や垂直条件について 日々是鍛錬 ひびこれたんれん




中2数学 平行四辺形の3大重要ポイント 映像授業のtry It トライイット
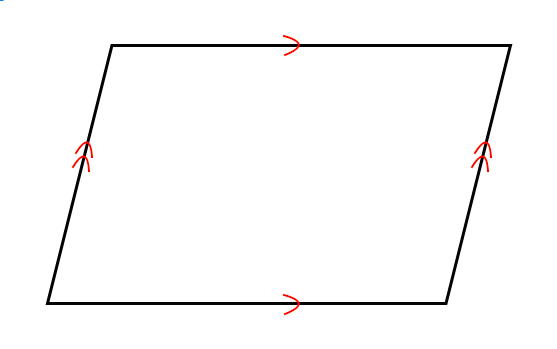



平行四辺形について知ろう 苦手な数学を簡単に



Q Tbn And9gcsn6zu4fidnkxqbvcuo7eumytehw6x Eltrnljczfdnugpofb91 Usqp Cau
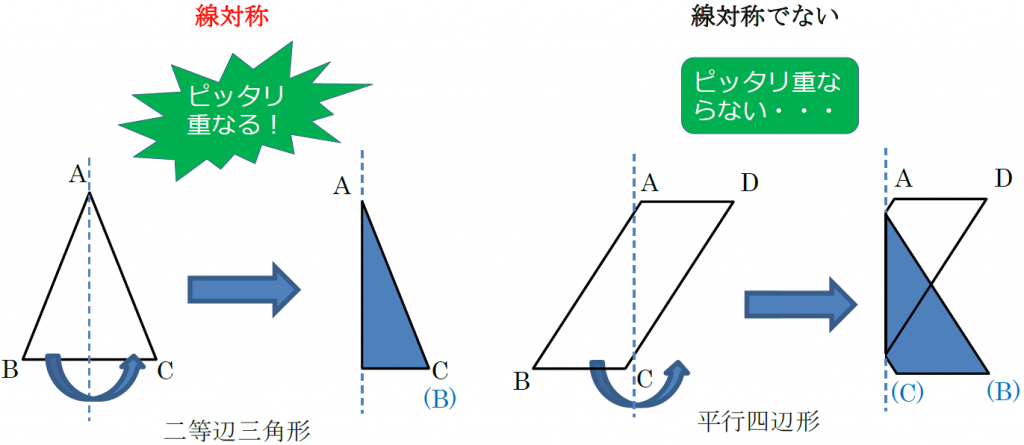



中1数学 点対称な図形とは まなビタミン
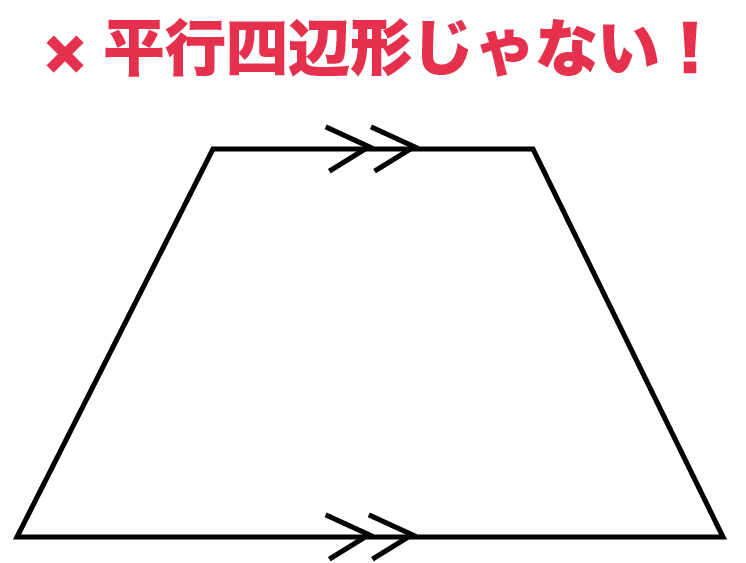



3分でわかる 平行四辺形の定義とは Qikeru 学びを楽しくわかりやすく




平行的定義與平行線間的距離 Live 多媒體數學觀念典online
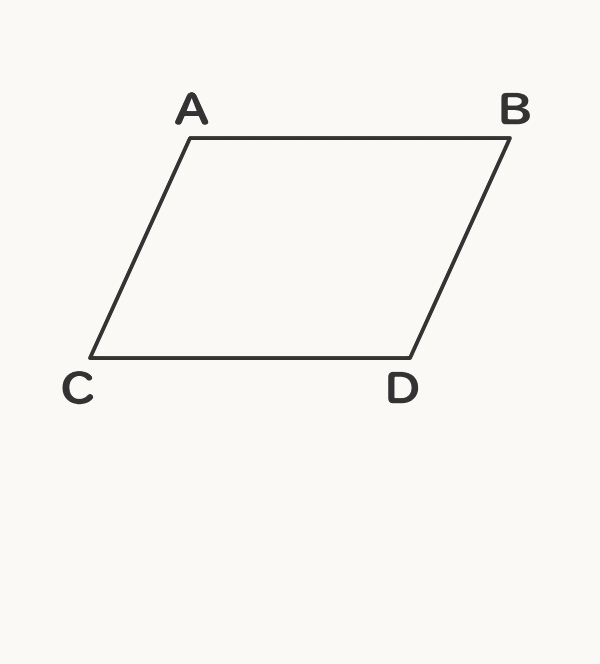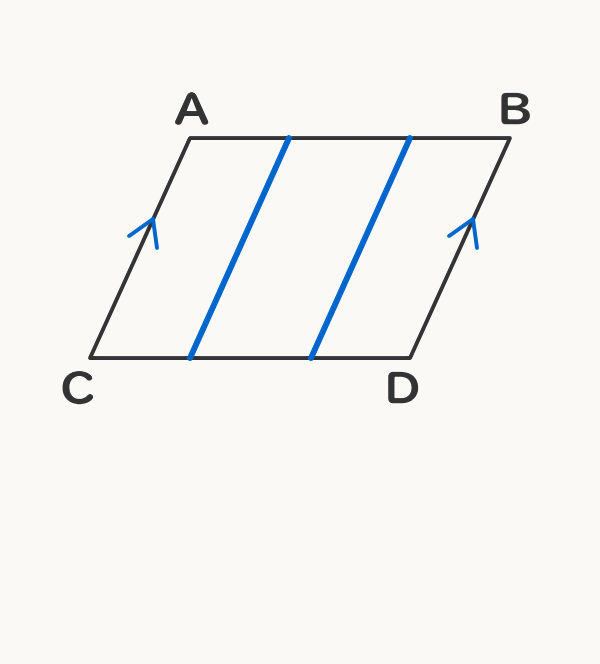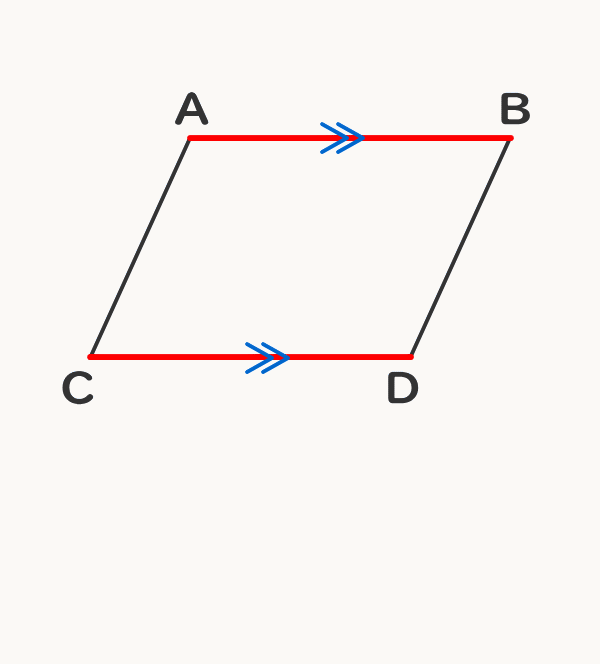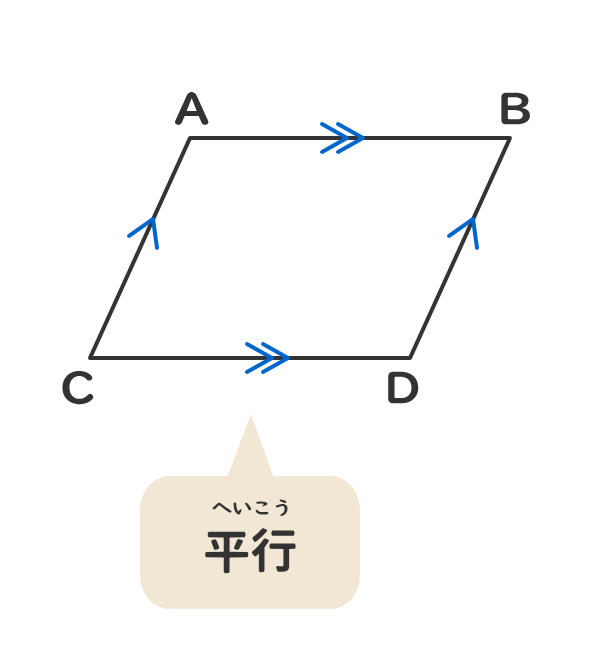



平行四辺形の仲間を知ろう 電験3種web
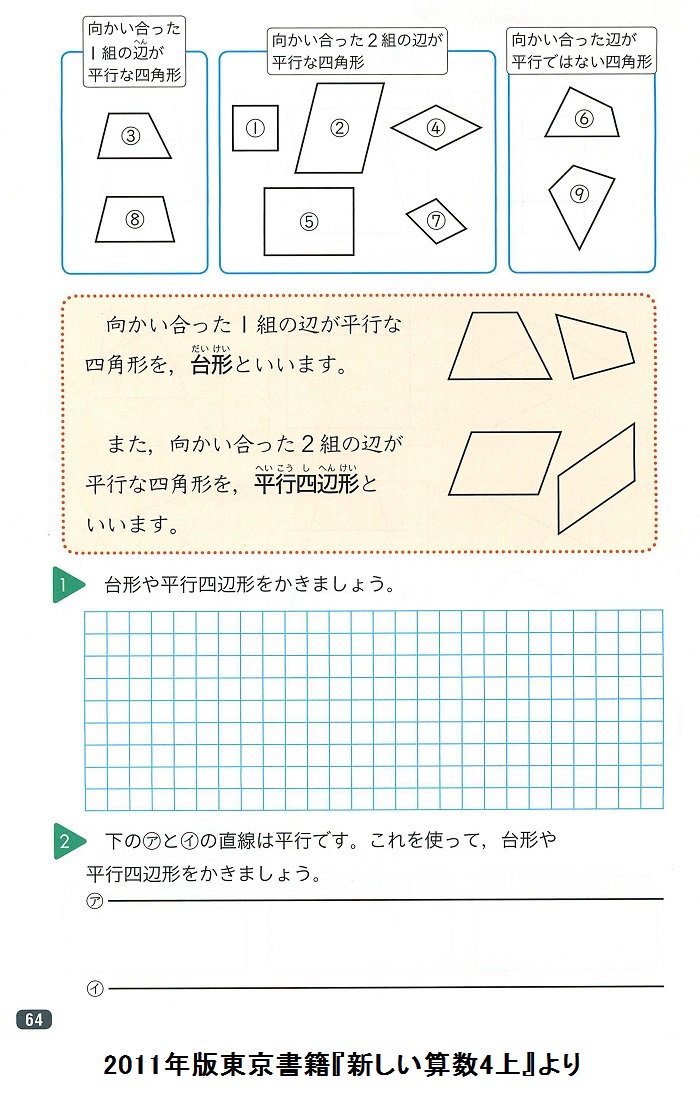



積分定数 掛算 台形と平行四辺形の定義について T Co G1tmmoxbkh それを教育するのにふさわしい発達段階は 中学校以降だと思います
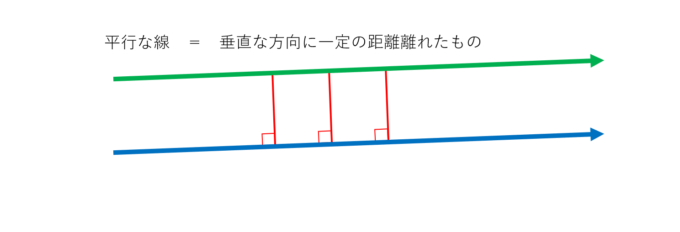



意外と知らない平行曲線のお話 数学 統計教室の和から株式会社



平行とは 1分でわかる意味 水平 垂直 並行との違い 建築物 曲線との関係




台形と平行四辺形の定義 ちがい 小岩 個別指導 元小学校教師が教える個別指導塾 できる子ども育成塾 小岩 篠崎の小学生専門 国語と算数の苦手を克服



Studydoctor2直線が平行になるための条件 中学2年数学 Studydoctor
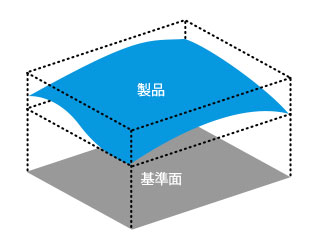



平行度 平面度について 竹内型材研究所



4年算数 垂直 平行と四角形 1 教え方のポイント
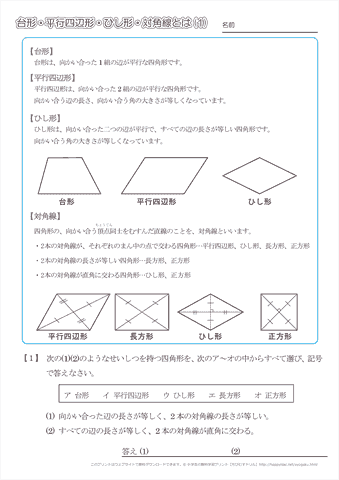



小学4年生の算数 台形 平行四辺形 ひし形 対角線 問題プリント ちびむすドリル 小学生




中2数学 平行四辺形の証明で知っておくべき5つの方法 映像授業のtry It トライイット



1
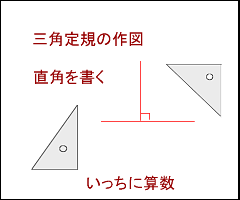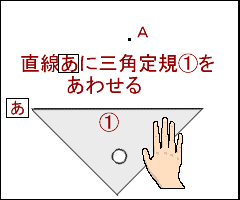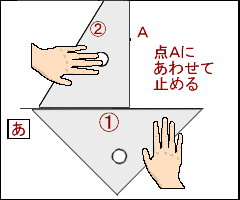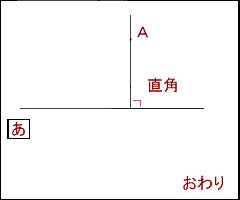



4年算数 垂直 平行と四角形 1 教え方のポイント




3分でわかる 平行四辺形の定義とは Qikeru 学びを楽しくわかりやすく




中学校数学 証明のコツ 年01月
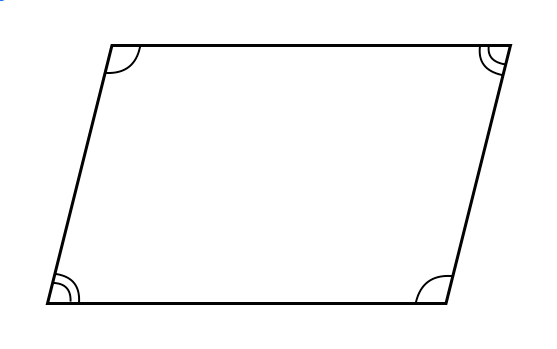



平行四辺形について知ろう 苦手な数学を簡単に
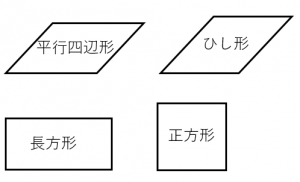



平行四辺形 ひし形 長方形 正方形の違い 具体例で学ぶ数学



1




直線の垂直 平行の関係 算数用語集
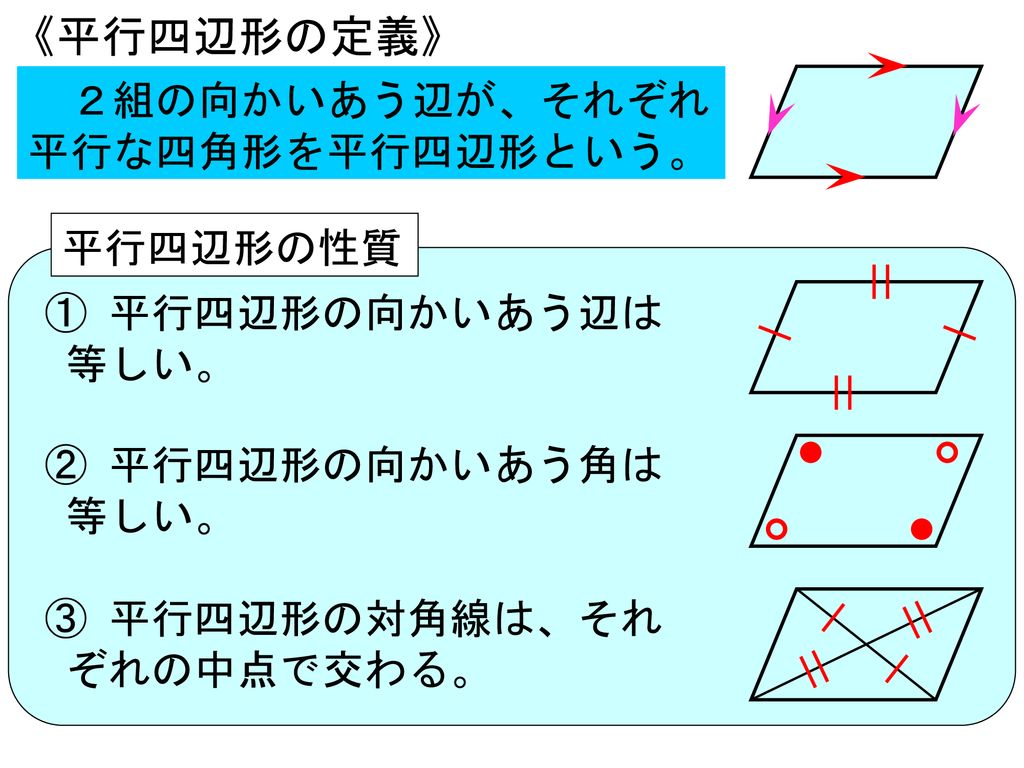



5 図形と合同 2章 平行四辺形 1 平行四辺形 5時間 Ppt Download



Http Mathmath Sakura Ne Jp 12mizutani Pdf



平行の条件と角度 中学から数学だいすき



高校入試と 平行四辺形の定義と定理について 中学生 受験対応 英語 数学 学習講座



3分でわかる 平行四辺形の定義とは Qikeru 学びを楽しくわかりやすく




高校数学の美しい物語の管理人 算数の本を書きました ルール 定義 と事実 定理 を区別してほしい というテーマ 算数の疑問 に自信をもって答えられるようになるはず 例 なぜ や より や を先に計算するのか なぜ 2 0 5 4 なのか




等脚台形の定義と性質 中学校数学の範囲内で考える 身勝手な主張



3分で分かる 平行四辺形とは 定義や性質 成立条件をわかりやすく 合格サプリ



Http Mixedmoss Com Noneuclidiangeometry Poincaremodel Chapter4 Parallel Parellel Pdf



中点連結定理を使った平行四辺形であることの証明 教遊者



大学数学の教科書の読み方 最初に 定義 命題 証明 を知ろう 趣味の大学数学




平行 Wikipedia



特別な平行四辺形 Youtube




平行度 平面度について 竹内型材研究所



平行の条件と角度 中学から数学だいすき



ベクトルの平行条件 垂直条件



壮大 平行 の 定義




直線と平面の位置関係 平行 垂直 ねじれの位置 数学fun




中2数学 平行四辺形 長方形 ひし形 正方形の違い 映像授業のtry It トライイット




平行四辺形の定義から性質と条件をわかりやすく証明 特に対角線の性質を押さえよう 遊ぶ数学



数学的に 平行線が決して交わらないことをどのように証明できますか Quora




中2 中2 数学 定義 合同条件 Etc 中学生 数学のノート Clear



平行移動とは 1分でわかる意味と定義 やり方 二次関数との関係




定義と定理 12月 年 光が丘中学校 ブログ 光が丘中学校




中学数学 特別な平行四辺形について Clear



台形とは 定義や公式 面積の求め方 面積比の計算問題 受験辞典



3分で分かる 平行四辺形とは 定義や性質 成立条件をわかりやすく 合格サプリ



外積ベクトルの定義と公式 3次元 理数系無料オンライン学習 Kori




直線と平面の位置関係 平行 垂直 ねじれの位置 数学fun




平行 と 並行 と 平衡 の違いとは 分かりやすく解説 意味解説辞典



平行の定義を教えてください まず 直線の定義を書きます ノ Yahoo 知恵袋




4年 算数 垂直 平行と四角形




ロイロノート スクール サポートページ 小4 算数 垂直と平行と四角形 実践事例 会津若松ザベリオ学園小学校




壮大 平行 の 定義



簡単にわかる ねじれの位置とは 苦手な数学を簡単に
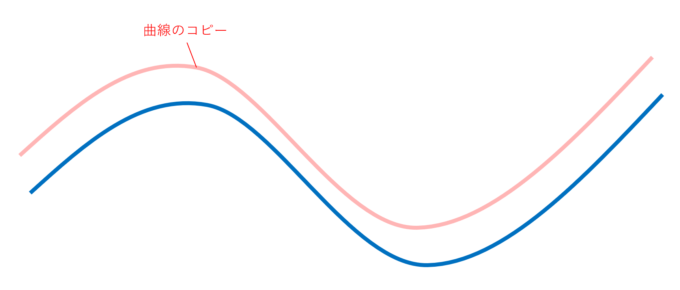



意外と知らない平行曲線のお話 数学 統計教室の和から株式会社
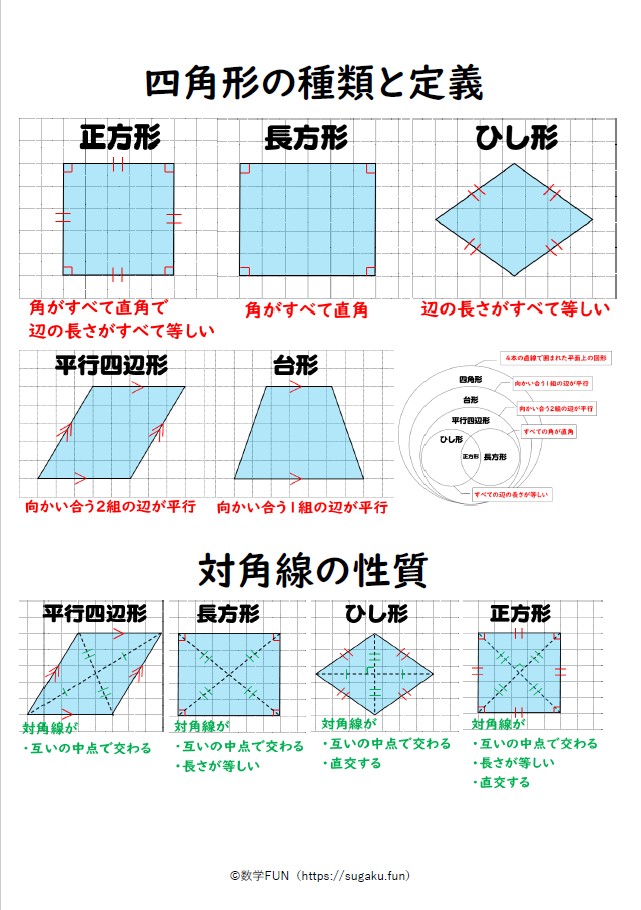



四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun



平行とは 1分でわかる意味 水平 垂直 並行との違い 建築物 曲線との関係




姿勢偏差の指示例と公差域の定義 幾何公差の基礎知識6 ものづくり まちづくり Btob情報サイト Tech Note




平行四辺形の定義 定理 性質 と証明問題 中学数学の図形 リョースケ大学



2直線の平行の定義に関する質問です まず質問を簡潔に述べると Yahoo 知恵袋



Corel Designer ヘルプ 投影された描画プレーンをインタラクティブに定義する
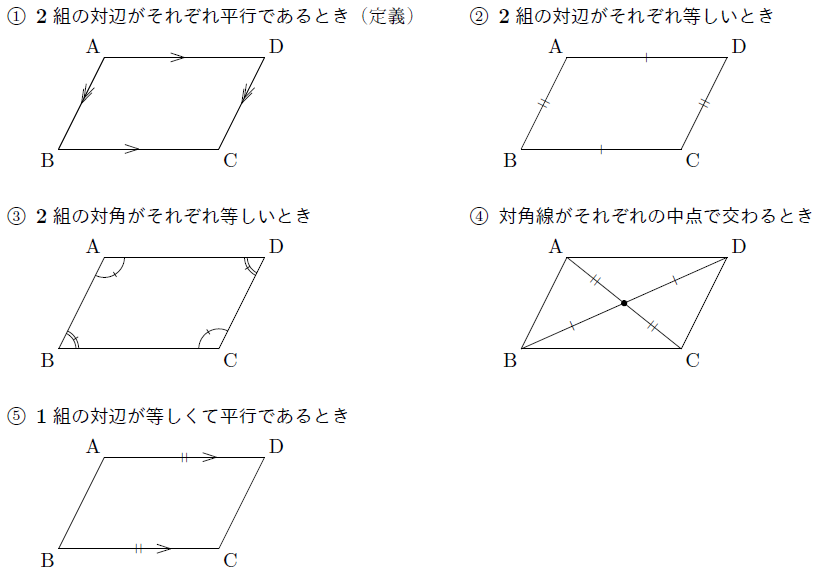



平行四辺形になるための条件 まなびの学園
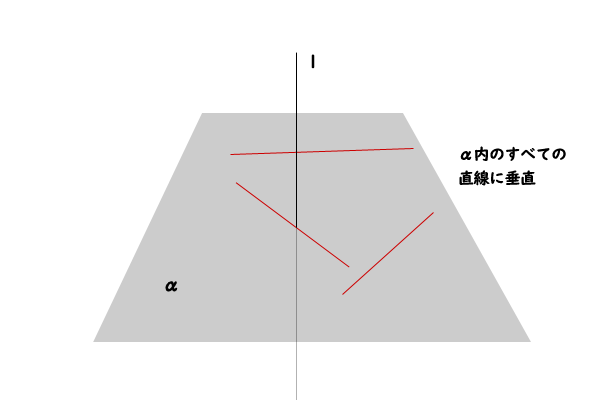



平面に垂直な直線 平面に直交する直線 垂線 について 高校数学マスター



0 件のコメント:
コメントを投稿